挑战强化学习后训练霸权！全新无监督方法仅需1条数据+10步优化

无需标注数据、无需繁琐奖励设计，只用 10 步就能见效——「熵最小化」或许比强化学习更适合大语言模型快速升级。

强化学习（RL）近年来在大语言模型（LLM）的微调中大获成功，但高昂的数据标注成本、复杂的奖励设计和漫长的训练周期，成为制约 RL 进一步应用的瓶颈。

Ubiquant 研究团队提出了一种极为简单有效的无监督方法—— One Shot 熵最小化（Entropy Minimization，EM），仅用一条无标签数据，训练 10 步内即可显著提升 LLM 性能，甚至超过使用成千上万数据的 RL 方法。

一、从 RL 到 EM：LLM 微调的困境与新思路

当前，大语言模型（LLM）在经过海量数据预训练后，展现出了惊人的通用能力。然而，要让模型在特定、复杂的推理任务（例如数学、物理或编程）上达到顶尖水平，后训练（post-training）主流后训练方法是采用强化学习（RL），特别是结合可验证奖励的强化学习（RLVR）。

尽管基于 RL 的微调在提升模型性能上取得了显著进展，但其过程却面临着一系列明显的弊端，使得这种方法成本巨大且过程繁琐。

RL，特别是 RLVR，对大规模高质量标注数据的依赖性极强。其次，RL 方法的成功在很大程度上取决于复杂且精心的奖励函数设计。

这需要专家知识来最大化优势信号并防止模型 " 奖励作弊 "。此外，许多常用的 RL 算法（如 PPO）需要额外的奖励模型，这不仅增加了算法复杂性，并且大量的大量的训练步骤和漫长的采样过程带来了巨额的计算开销。

相较之下，熵最小化（EM）提出了一种全新的思路。EM 的核心理念是无需任何标注数据或外部监督来训练模型。它仅依赖模型自身预测分布的熵（entropy）进行优化。

具体而言，EM 训练模型将其概率质量更多地集中在其最自信的输出上。EM 背后的核心思想基于一个关键假设和一个简单直觉：如果一个模型本身足够有能力，那么当它对其预测结果更 " 自信 " 时，它也更有可能是正确的。

换句话说，正确答案通常比错误答案具有更低的熵值。通过优化目标来降低模型生成序列的熵，EM 促使模型变得更加 " 自信 "，从而强化其在预训练阶段已经获得的能力

二、熵最小化（EM）到底怎么做？

具体来说，熵最小化方法的核心公式为：

设表示一个预训练自回归语言模型 p θ 的词汇表，该模型由参数 θ 定义。给定一个输入提示 x（例如一个问题或问题描述），模型根据其当前策略自回归地生成一个响应序列 y= ( y1,y2, … ,yT )

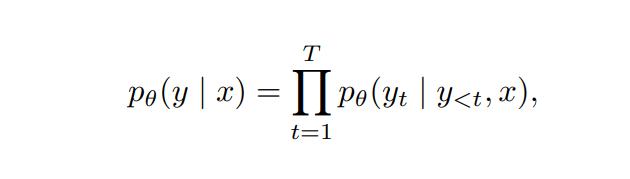
其中 T 是生成序列的长度。核心思想是通过在每一步生成时最小化标记级别的熵，来减少模型对其自身预测的不确定性。时间步 t 的条件熵定义为：

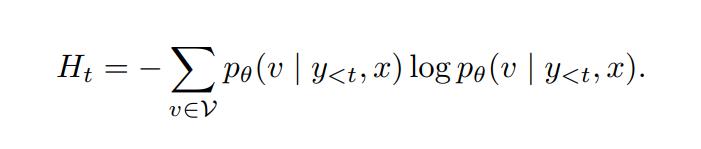
单个输入 x 的总体 EM 损失由以下公式给出：

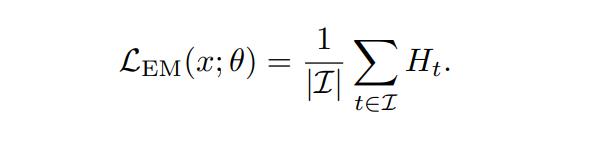
简单而言，这个损失函数鼓励模型提高对自身预测的信心，无需依赖外部监督信号或奖励函数。由于其完全依赖于模型本身而非外部信号，和预训练目标完全兼容，在有效简化优化过程的同时可能带来潜在对于模型内一致性的破坏。

三、为何只用一条示例就足够？

熵最小化的成功高度依赖示例的选择。熵最小化（EM）依赖于模型的预测不确定性可以作为有意义的训练信号。

然而，并非所有输入提示在这方面都同样具有信息量。

因而研究者采用了一种基于模型表现方差的示例筛选方法：通过计算模型多次生成结果的准确性方差，挑选那些模型表现不稳定的示例进行训练。

这种方差量化了模型对给定输入的预测不一致性。低方差意味着要么对正确性有高度信心（接近完美的成功），要么对失败有高度信心（完全错误）。

相反，表现方差大的示例更能有效驱动模型降低熵值、明确决策边界。这也是为何只用一条高质量示例，就能快速推动模型的推理性能。

研究人员使用的唯一一条样本如下：

Problem: The pressure P exerted by wind   on   a sail varies jointly as the area A of the sail and the cube of the wind ’ s velocity V. When the velocity is   8   miles per hour, the pressure   on   a sail of   2   square feet is   4   pounds. Find the wind velocity when the pressure   on   4   square feet of sail is   32   pounds.Solution:   12.8

四、实验结果：以小博大，性能媲美甚至超越 RL

研究人员在多个数学推理任务上测试了熵最小化（EM）的效果。结果显示，仅一条示例、10 步训练，EM 方法即大幅提高了 Qwen2.5-Math-7B 的性能：

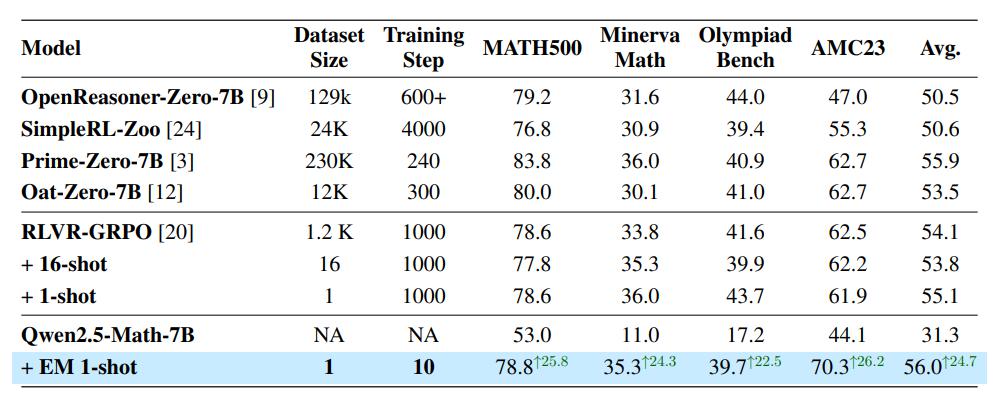
MATH500 测试集：

准确率从 53% 提升到 78.8%，提升 25.8 个百分点；

Minerva Math 测试集：

准确率从 11% 提升到 35.3%，提升 24.3 个百分点；

AMC23 测试集：

准确率从 44.1% 提升到 70.3%，提升 26.2 个百分点。

更令人瞩目的是，即使只使用一个示例和极少的训练步骤（仅仅 10 步），EM 方法极大地缩小了 Qwen2.5-Math-7B 与 Prime-Zero-7B 和 RLVR-GRPO 等先进的基于 RL 的模型之间的差距。

特别是在 AMC23 基准测试中，经过 EM 增强的 Qwen2.5-Math-7B 达到了具有竞争力的 70.3 分，逼近领先的 RL 模型这些结果清晰地表明，熵最小化（EM），尽管比典型的强化学习方法更简单、数据效率更高，但在增强基础语言模型在数学推理任务上的性能方面，具有巨大的潜力。那么为什么熵最小化能这么有效果呢？熵在模型的训练和推理过程中起到什么样的作用呢？

五、EM vs. RL：深入分析 " 置信度 " 与 "Logits 偏移 "

大语言模型在生成每个 token 时，会先产生一组未经归一化的分数，称为 Logits。这些 Logits 随后通过 Softmax 函数转换为概率分布，决定了下一个 token 的选择。

因此，Logits 的分布形态直接反映了模型对其预测的 " 置信度 " 和对不同 token 的偏好。这项研究通过对模型 Logits 分布的深入分析发现，熵最小化（EM）和强化学习（RL）对模型内部置信度的影响方向截然相反。

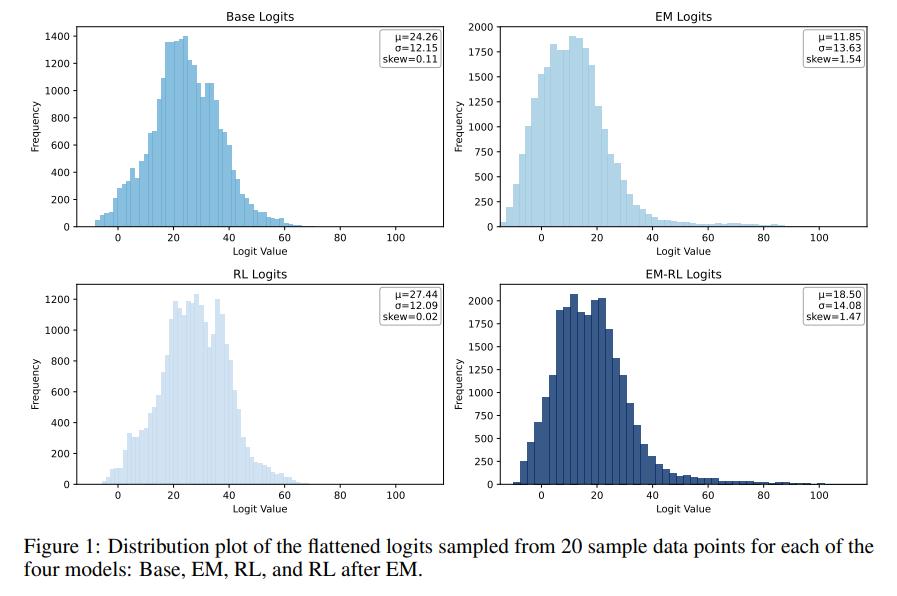
EM：向右偏移，强化自身自信

研究表明，经过 EM 训练的模型，其 Logits 分布会显著地向右偏移。这种右移意味着模型在生成过程中，会反复强化自身的预测置信度。模型将更多的概率质量集中在少数它认为 " 确定 " 的 token 上，使得原本高概率的区域进一步向高分区间扩展。

直观来说，这让模型对其最看好的答案变得更加 " 自信 "。

在生成和采样时，这种向右的 Logits 偏移是有益的。它增加了高概率的候选 token 数量，扩展了模型能够遵循的 " 高概率路径 "，从而潜在地增强了模型的整体生成能力。

实验中，EM 训练后的模型在评估时表现出与采样温度的相反趋势：随着温度升高，性能下降。这可以用贪婪解码（即总是选择概率最高的 token）来解释——因为 EM 训练将概率质量高度集中在少数确定性 token 上，贪婪解码在这种分布下变得非常有效。

RL：向左偏移，受真实信号引导

与 EM 不同，经过 RL 训练的模型则表现出 Logits 分布向左偏移的趋势。研究者推测，这是受到训练过程中 " 真实 "（ground-truth）信号的影响 2。

RL 通过外部奖励函数来调整模型的行为，它会惩罚那些模型预测概率很高但与地面真实不符的 token。

通过对这些高概率但不正确的 token 进行降权（reranking），RL 降低了它们的排序，从而导致整体 Logits 分布向左偏移。RL 训练后，即使经过 reranking，这些原本低概率的 token 往往只占据概率分布中的中间位置，需要更高的采样温度才能被选中。

因此，RL 训练的模型表现出与 EM 相反的趋势：性能随着采样温度的升高而提升。

虽然 RL 的目标是提升模型性能，但其导致的 Logits 左移被认为对大语言模型的生成过程有害，因为它减少了采样时的高概率路径数量，可能会削弱模型的整体性能。

这种 Logits 偏移的差异，通过分析 Logits 分布的偏度（Skewness）得以量化。

EM 训练显著提高了 Logits 分布的偏度，呈现右偏；而 RL 训练则显著降低了偏度，甚至导致左偏。即使在 EM 后再进行 RL 训练，Logits 分布的偏度也会从 EM 后的高值有所下降，遵循 RL 的趋势。

这样的差异和塑造了 EM 和 RL 完全不同的推理采样策略。

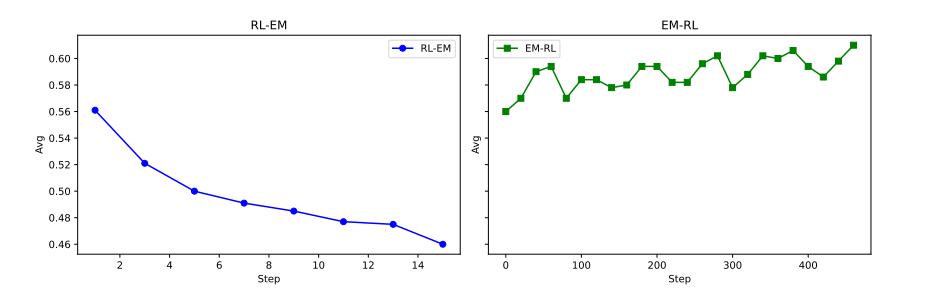
在评估阶段，随着采样温度的升高，EM 模型在四个数学推理基准测试上的平均表现持续下降。

这一趋势与上图中展示的经过强化学习（RL）训练的模型形成鲜明对比，后者在更高的采样温度下往往表现更佳。EM 更像是一个分布塑造工具（distribution shaping tool），通过强化模型自身的内在一致性来提升置信度，从而重塑了现有知识的分布。

六、" 过度自信 " 的陷阱与随机性

研究也揭示了这种高效性背后隐藏的 " 陷阱 " ——即 " 过度自信 " 现象。

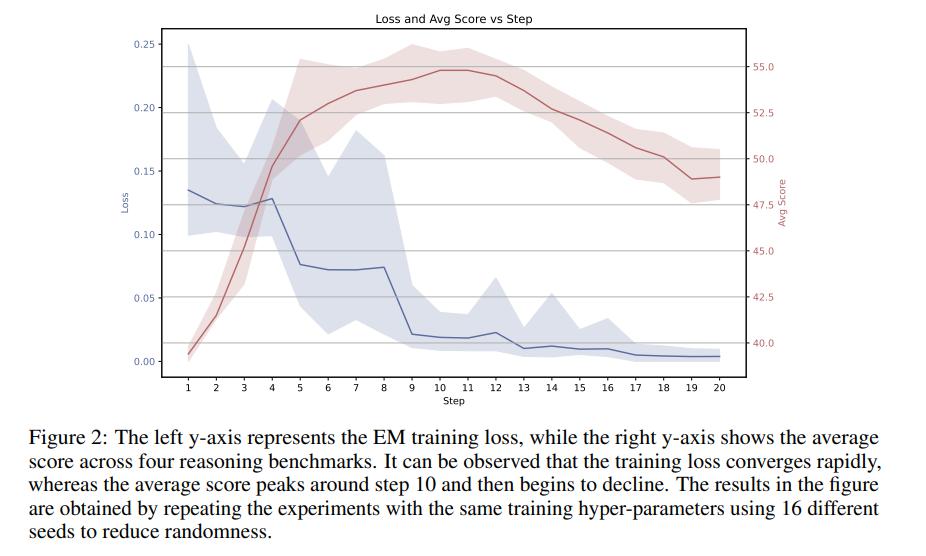
训练初期，EM 训练损失迅速下降，模型的数学推理性能也随之提升然而，大约在训练进行到 10 步左右时，模型的性能达到了顶峰。令人意外的是，即使 EM 训练损失继续下降，模型的数学推理性能反而开始下降。

这种 " 过度自信 " 被认为是由于持续的 EM 训练过度放大了模型在推理过程中对其自身生成 token 的置信度。持续的 EM 训练可能会过度强化模型已有的先验偏差，导致输出结果过度集中于狭窄、过度自信的 token 分布，从而加剧算法偏差并导致输出显著偏离正确路径，最终损害了模型的实际推理性能。

熵最小化的不稳定性和过度自信的损害也体现在训练时的温度上。经过 EM 训练的模型在四个数学推理基准上的平均性能随着生成温度的升高总体呈现上升趋势。

平均性能的最大值最初增加，随后在温度约为 0.5 时开始下降。较高的温度带来更好的平均推理能力，而适中的温度（如 0.5）则导致更大的性能波动，从而为更高的峰值性能创造了机会。

EM 训练同时展现出显著的随机性，即便设置完全相同，四个数学推理基准测试的平均得分也会因种子不同而相差高达两倍。

七、EM 适合哪些场景？

研究表明，熵最小化（EM）尤其适合：

尚未进行大量 RL 调优的基础模型或仅经过 SFT 的模型：

研究在多个不同的基础模型上评估了 One-shot EM 的效果，结果表明，仅通过单个示例和极少的训练步数，EM 能够持续且显著地提升这些模型在数学推理基准测试上的性能。

然而，研究也发现，当应用于已经过大量 RL 广泛微调的模型（如 SimpleRL-Zoo）时，One-shot EM 反而可能导致性能下降 5。这与在 RL 之后应用 EM 可能锁定狭窄、过度自信的输出模式并损害性能的发现一致。

需要快速部署、没有充足标注数据或资源有限的场景。

EM 的核心优势在于其极高的效率和对数据的极低需求，研究发现，One-shot EM 实际上比 Multi-shot EM 表现出更好的性能和更强的泛化能力。

尽管 Multi-shot 使用了更多的示例，但 One-shot EM 通过单个示例实现了更稳定和细致的优化。有效减少了样本偏差并缩小了输出方差。这进一步强化了 EM 在数据极度稀缺场景下的吸引力。

无代价能力增强：

熵最小化（EM）可以作为现有后训练范式的有力补充甚至起点。将 EM 应用在 RL 之前能够带来有效增益，使其成为 RL 的有效 " 启用基础 "。

EM 通过其独特的 Logits 右偏移效应提升模型的自信度，增强模型的推理能力，并可能促进后续 RL 训练的更快收敛和更稳定优化。

对于已经深度调优过的 RL 模型，再使用 EM 反而可能带来性能的下降。

八、行业前景与未来研究

One-shot EM 的成功，不仅在于其惊人的数据和计算效率，还在于它为 LLM 后训练提供了一种完全无监督的、可落地的替代方案，它不需要人工标注数据，不需要构建复杂的奖励模型，极大地降低了后训练的门槛和成本。这项研究同样为未来的探索打开了广阔的空间：

训练稳定性与鲁棒性：

One-shot EM 虽然高效，但也伴随超参数敏感性和一定的训练不稳定性。研究发现，持续的 EM 训练可能会导致模型 " 过度自信 "，反而损害性能。未来的工作需要探索早停标准或自适应调度机制，以及减少训练的随机性，以进一步稳定和提升 EM 的效果。

泛化能力与跨领域应用：

EM 在数学推理任务上表现出色，但它能否泛化到对话、摘要、代码生成等其他领域？这需要进一步的实验验证。同时，当前 EM 在 Token 级别操作，未来的研究可以探索在序列或语义单元上应用结构化熵，或引入任务特定先验知识和自适应熵正则化，以释放更多潜力。

与现有技术的融合：

EM 作为一种分布塑造工具，与 SFT、RLHF 等现有后训练技术概念上正交。研究发现，在 RL 之前应用 EM 可以带来有益的对数分布偏移。

未来的工作可以系统地研究不同的 EM 与 RL 结合的时间表、课程策略及其相互作用，探索构建更强大混合方法的可能性。EM 甚至可以作为 SFT 或 RLHF 过程中的一种正则化策略，或作为现有模型的 " 信心压缩 " 层。

研究人员对置信度校准的深入研究结果还暗示，EM 通过强化高概率推理路径来增强模型的置信度。

这表明 EM 可能是一种轻量级的信心校准方法。未来的研究需要开发更精确的评估协议来量化 EM 的校准效应，深入理解其背后的机制。

（本文内容参考自论文《One-shot Entropy Minimization》，详细实验与数据参见原文。）

一键三连「点赞」「转发」「小心心」

欢迎在评论区留下你的想法！

—  完  —

点亮星标

科技前沿进展每日见